Лосяш, увлечённый астрономией, решил исследовать звёздное небо и провести кластеризацию звёзд по их расположению на карте. Каждая звезда представлена точкой на графике, а кластер звёзд – это набор точек, лежащих внутри квадрата со стороной длиной 
. Каждая звезда обязательно принадлежит только одному из кластеров.
Центр звёздного скопления – это одна из звёзд, сумма расстояний от которой до всех остальных звёзд в кластере минимальна. Лосяш считает, что эта звезда является ключевой для понимания структуры скопления.
Под расстоянием понимается расстояние Евклида между двумя точками 
и 
на плоскости, которое вычисляется по формуле:
В файле А хранятся данные о шести кластерах звёзд, где 
для каждого кластера. В каждой строке записана информация о расположении одной звезды: сначала координата 
, затем координата 
. Значения даны в условных единицах, которые представлены вещественными числами. Известно, что количество звёзд не превышает 1000.
В файле Б хранятся данные о пяти кластерах звёзд, где 
для каждого кластера. Известно, что количество звёзд не превышает 10000. Структура хранения информации о звёздах в файле Б аналогична файлу А.
Для каждого файла определите координаты центра звёздного скопления каждого кластера, затем вычислите два числа: 
– среднее арифметическое абсцисс центров звёздных скоплений, и 
– среднее арифметическое ординат центров звёздных скоплений.
В ответе запишите четыре числа через пробел: сначала целую часть произведений 
и 
для файла А, далее целую часть произведения 
и 
для файла Б.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию. Для выполнения задания используйте данные из прилагаемого файла.
Для начала визуально оценим данные в условии кластеры. Для этого откроем предложенные файлы в 
, перейдем в раздел «Вставка 
Диаграммы 
Точечная».
Диаграмма для файла А имеет вид:
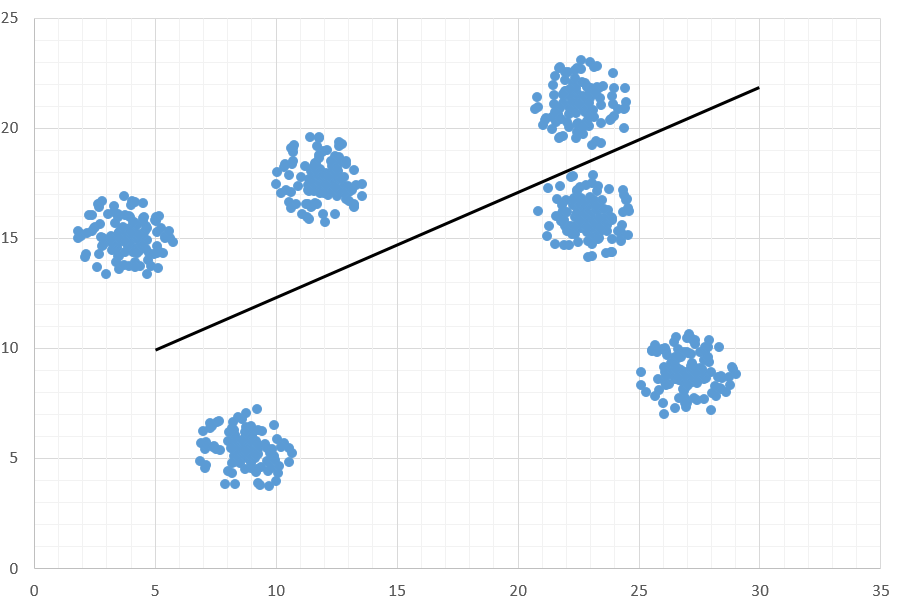
Рассмотрим 6 кластеров и координаты, которыми их можно последовательно отделить. Верхние 3 кластера от нижних отделим прямой, проходящей через точки 
и 
. Уравнение этой прямой будет 
. Верхние 3 кластера между собой разделим по значениям 
и 
:
1) 2)
3)
Для нижних 3 кластеров используем:
4) 5)
6) все остальные точки
Код программы для файла А:
file = open("3_A.txt")
clusters = [[] for _ in range(6)]
for star in file:
x, y = list(map(float, star.strip().split()))
if 0.48 * x + 7.6 > y and y > 13:
clusters[0].append((x, y))
elif 0.48 * x + 7.6 > y and x > 20:
clusters[1].append((x, y))
elif 0.48 * x + 7.6 > y and x < 15:
clusters[2].append((x, y))
elif x > 20:
clusters[3].append((x, y))
elif x < 7:
clusters[4].append((x, y))
else:
clusters[5].append((x, y))
sum_x = sum_y = 0
for cluster in clusters:
tx = ty = 0
mn = 10 ** 20
for centroid in cluster:
x1, y1 = centroid
sm = 0
for star in cluster:
x2, y2 = star
sm += ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5
if sm < mn:
mn = sm
tx, ty = x1, y1
sum_x += tx
sum_y += ty
P_x = sum_x / len(clusters)
P_y = sum_y / len(clusters)
print(int(P_x * 100), int(P_y * 100))
Диаграмма для файла Б имеет вид:
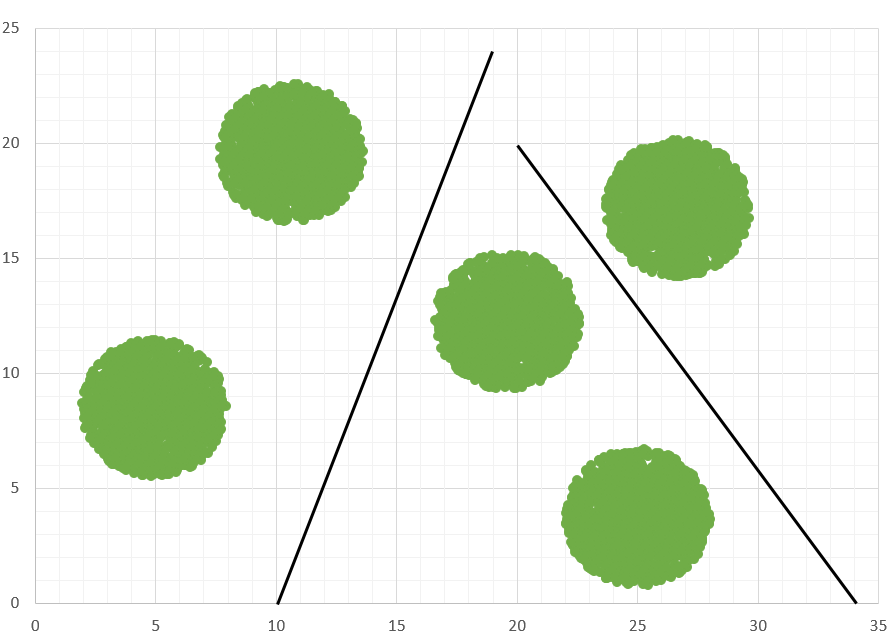
Рассмотрим 5 кластеров и координаты, которыми их можно последовательно отделить. Для удобства разделим прямыми кластеры на группы: два левых, два средних, самый правый.
Самый правый кластер можно отделить прямой проходящей через точки 
и 
. Уравнение этой прямой будет 
.
Два средних кластера можно отделить от остальных с помощью предыдущей прямой и прямой, проходящей через точки 
и 
. Уравнение этой прямой будет 
. Между собой кластеры группы отделим по координатам 
и Оставшиеся два кластера отделим по условиям:
1) 
2) все остальные точки
Код программы для файла Б:
file = open("3_B.txt")
clusters = [[] for _ in range(5)]
for star in file:
x, y = list(map(float, star.strip().split()))
if (-10 / 7) * x + 340 / 7 < y:
clusters[0].append((x, y))
elif (-10 / 7) * x + 340 / 7 > y and (8 / 3) * x - 80 / 3 > y and y < 8:
clusters[1].append((x, y))
elif (-10 / 7) * x + 340 / 7 > y and (8 / 3) * x - 80 / 3 > y and y > 9:
clusters[2].append((x, y))
elif y < 15:
clusters[3].append((x, y))
else:
clusters[4].append((x, y))
sum_x = sum_y = 0
for cluster in clusters:
tx = ty = 0
mn = 10 ** 20
for centroid in cluster:
x1, y1 = centroid
sm = 0
for star in cluster:
x2, y2 = star
sm += ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5
if sm < mn:
mn = sm
tx, ty = x1, y1
sum_x += tx
sum_y += ty
P_x = sum_x / len(clusters)
P_y = sum_y / len(clusters)
print(int(P_x * 100), int(P_y * 100))
