Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике, образующий звезду на небесном полотне. Каждая звезда обязательно принадлежит только одному из кластеров.
Также на звёздном небе присутствует пучок звёзд, образующий синусоиду. Кластер звёзд может считаться принадлежащим синусоиде, если график синусоиды проходит сквозь кластер
Истинный центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна.
Под расстоянием понимается расстояние Евклида между двумя точками 
и 
на плоскости, которое вычисляется по формуле:
В файле A хранятся данные о звёздах четырёх кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата 
, затем координата 
. Значения даны в условных единицах, которые представлены вещественными числами. Известно, что количество звёзд не превышает 5500.
В файле Б хранятся данные о звёздах восьми кластеров. Известно, что количество звёзд не превышает 35000. Структура хранения информации о звёздах в файле Б аналогична файлу А.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: 
– среднее арифметическое абсцисс центров кластеров, и 
– среднее арифметическое ординат центров кластеров. Кластеры, принадлежащие синусоиде, в вычислениях не учитывать.
В ответе запишите четыре числа через пробел: сначала целую часть произведений 
и 
для файла А, далее целую часть произведения 
и 
для файла Б.
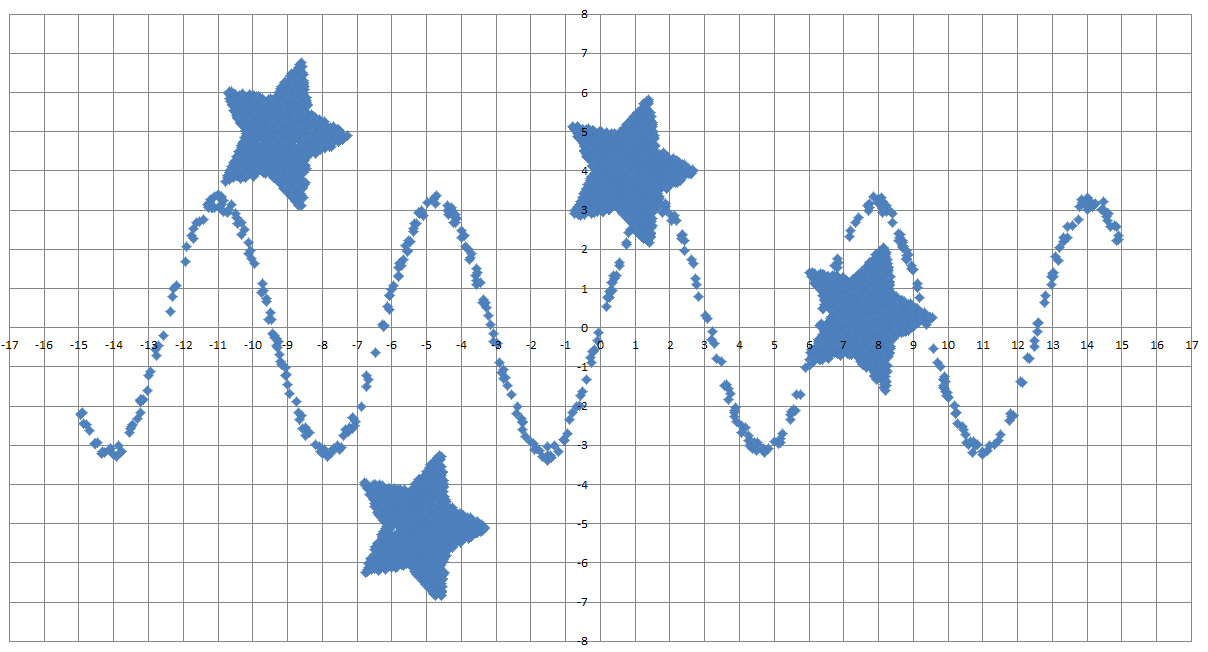
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию. Для выполнения задания используйте данные из прилагаемого файла.
Для начала визуально оценим данные в условии кластеры. Для этого откроем предложенные файлы в 
, перейдем в раздел «Вставка 
Диаграммы 
Точечная».
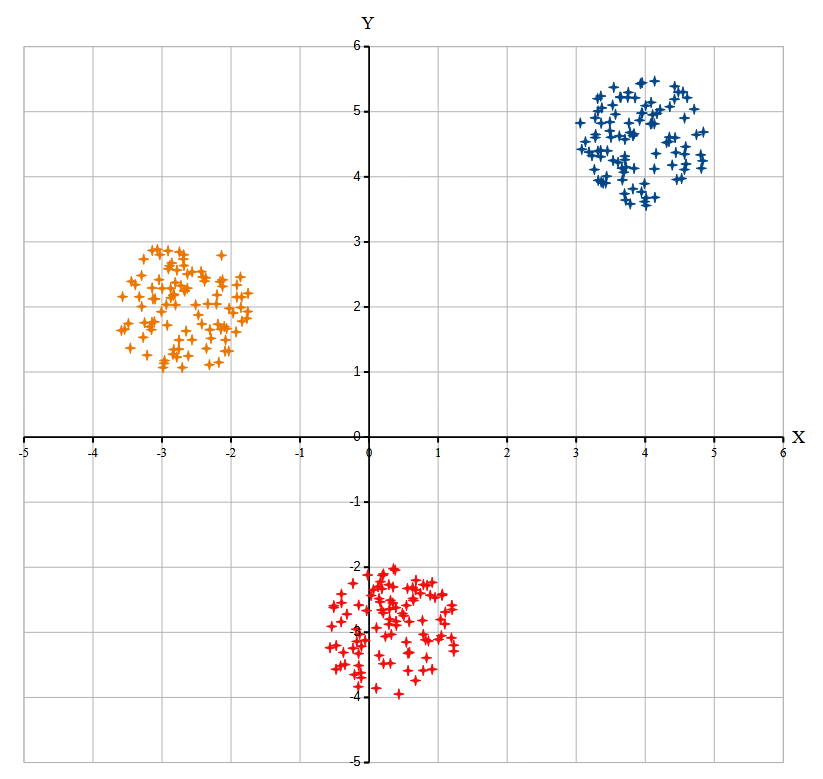
Диаграмма для файла А имеет вид:
Просто разделить кластеры с помощью прямых не получится. Воспользуемся методом DBSCAN:
Код программы для файла А:
from math import *
f = open(’1A.txt’)
s = f.readline()
a = [list(map(float, i.replace(’,’, ’.’).split())) for i in f]
# Вначале находим по одной точке в файле, принадлежащей каждому кластеру - это будет начальная точка для кластера
# Отобрать их можно либо анализом первых точек в Excel файле, либо программным способом
# Также нужно учесть, что кластер может принадлежать синусоиде
cl = [[[a[0][0], a[0][1]]], [[a[4286][0], a[4286][1]]]]
a.pop(4286), a.pop(0)
for k in range(2):
for j in cl[k]:
for i in range(len(a)):
if a[i] != ’*’:
p = [a[i][0], a[i][1]]
if dist(p, j) < 0.4:
cl[k].append(p)
a[i] = ’*’
sum_x = sum_y = 0 # Переменные для суммы абсцисс и ординат центров
for i in cl:
tx = ty = 0 # Координаты текущего центра кластера
mn = 100000050000 # Минимальное расстояние
for j in i:
x1, y1 = j
sm = 0 # Суммарное расстояние
for k in i:
x2, y2 = k
sm += ((x2-x1)**2 + (y2-y1)**2)**0.5
if sm < mn:
mn = sm
tx, ty = x1, y1
sum_x += tx
sum_y += ty
print(int(sum_x / 2 * 100))
print(int(sum_y / 2 * 100))
Диаграмма для файла Б имеет вид:
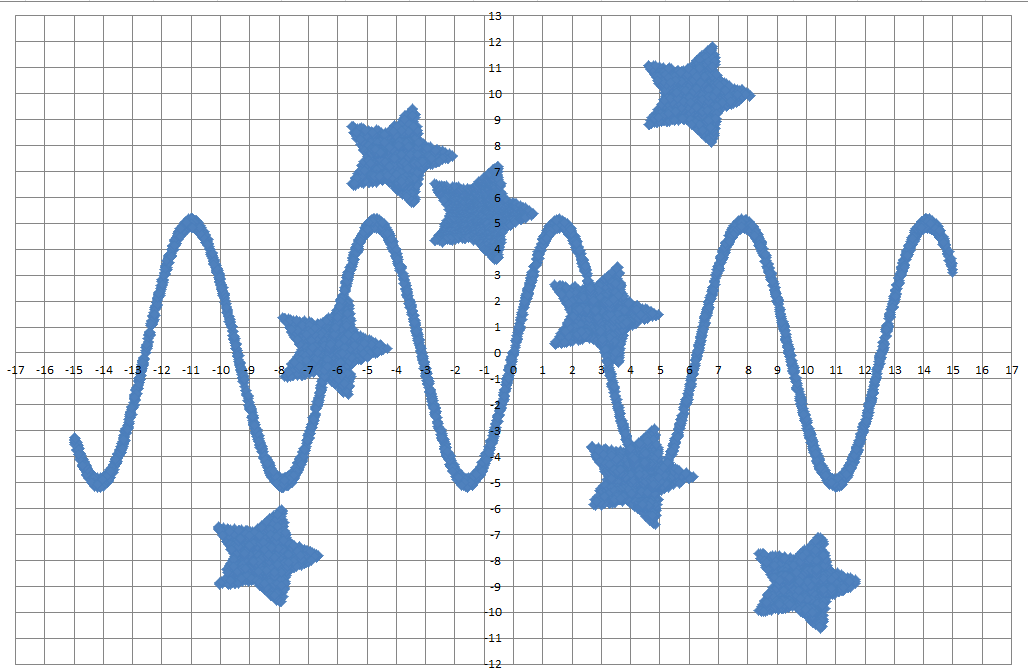
Просто разделить все кластеры с помощью прямых не получится. Воспользуемся методом DBSCAN:
Код программы для файла Б:
from math import *
f = open(’1B.txt’)
s = f.readline()
a = [list(map(float, i.replace(’,’, ’.’).split())) for i in f]
# Вначале находим по одной точке в файле, принадлежащей каждому кластеру - это будет начальная точка для кластера
# Отобрать их можно либо анализом первых точек в Excel файле, либо программным способом
# Также нужно учесть, что кластер может принадлежать синусоиде
cl = [[[a[3779][0], a[3779][1]]], [[a[33773][0], a[33773][1]]], [[a[4][0], a[4][1]]], [[a[0][0], a[0][1]]], [[a[3785][0], a[3785][1]]]]
a.pop(33773), a.pop(3785), a.pop(3779), a.pop(4), a.pop(0)
for k in range(5):
for j in cl[k]:
for i in range(len(a)):
if a[i] != ’*’:
p = [a[i][0], a[i][1]]
if dist(p, j) < 0.4:
cl[k].append(p)
a[i] = ’*’
sum_x = sum_y = 0 # Переменные для суммы абсцисс и ординат центров
for i in cl:
tx = ty = 0 # Координаты текущего центра кластера
mn = 100000050000 # Минимальное расстояние
for j in i:
x1, y1 = j
sm = 0 # Суммарное расстояние
for k in i:
x2, y2 = k
sm += ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5
if sm < mn:
mn = sm
tx, ty = x1, y1
sum_x += tx
sum_y += ty
print(int(sum_x / 5 * 1000))
print(int(sum_y / 5 * 1000))
