Задача к ЕГЭ по информатике на тему «задачи под вебы» №19

Автор admin На чтение 1 мин Просмотров 31

Задача с сайта https://kpolyakov.spb.ru/

На числовой прямой даны два отрезка: P = [3, 15] и Q = [14, 25]. Укажите наибольшую возможную длину такого отрезка А, что формула

((x ∈ P ) ≡ (x ∈ Q )) → ¬ (x ∈ A))

тождественно истинна, то есть принимает значение 1 при любом значении переменной x.

Раскроем импликацию по формуле:

a → b = ¬a∨ b

Тогда выражение принимает вид:

((x ∈ P) ⁄≡ (x ∕∈ Q))∨ (x ∕∈ A)

Находим x, при которых формула даёт ложь:

(x ∈ P ) ≡ (x ∈ Q)

Это выражение будет истинно в двух случаях: когда обе части дают ложь, либо когда обе части дают истину.

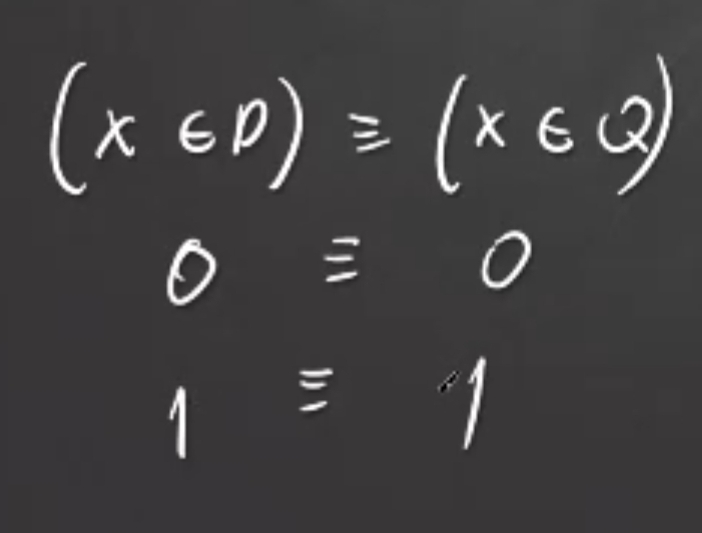
Нарисуем числовую прямую, изобразим на ней отрезки P и Q и отметим область, в которой наше выражение ложно.

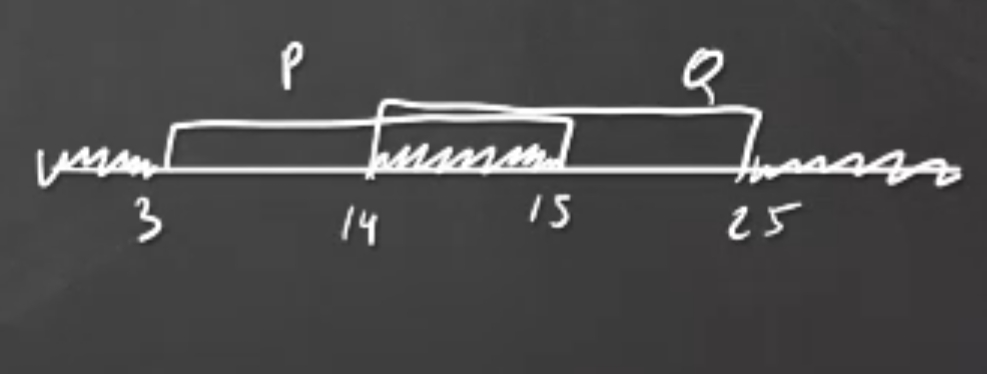
Получаем два варианта отрезка A:

$A = [13,14)$ или $A = (15,25]$

По условию задачи требуется найти наибольшую возможную длину отрезка А, поэтому выбираем первый отрезок и его длина: $14− 3 = 11$ .

Ответ: 11