Задача к ЕГЭ на тему «Функции. Исследование функции на возрастание/убывание» №6

Найдите все значения параметра $a$ , при каждом из которых уравнение

√ -- 2x3−3x2+4 + (a − 10) ⋅ ( 2)x3− 3x2+4 + 12 − a = 0

имеет шесть различных решений.

Сделаем замену $√ -- 3 2 ( 2)x −3x +4 = t$ , $t > 0 » class=»math» width=»auto»>. Тогда уравнение примет вид </p> <p> <center class=$ $t2 + (a − 10)t + 12 − a = 0 (∗)$ Будем постепенно выписывать условия, при которых исходное уравнение будет иметь шесть решений.
Заметим, что квадратное уравнение $(∗)$ может максимум иметь два решения. Любое кубическое уравнение $Ax3 + Bx2 + Cx + D = 0$ может иметь не более трех решений. Следовательно, если уравнение $(∗)$ имеет два различных решения (положительных!, так как $t$ должно быть больше нуля) $t1$ и $t2$ , то, сделав обратную замену, мы получим:

⌊ √ --x3−3x2+4 ( 2) = t1 ⌈ √ -- ( 2)x3−3x2+4 = t2

Так как любое положительное число можно представить как $√ -- 2$ в какой-то степени, например, $√ -- t1 = ( 2)log√2t1$ , то первое уравнение совокупности перепишется в виде

x3 − 3x2 + 4 = log√-t1 2

Как мы уже говорили, любое кубическое уравнение имеет не более трех решений, следовательно, каждое уравнение из совокупности будет иметь не более трех решений. А значит и вся совокупность будет иметь не более шести решений.
Значит, чтобы исходное уравнение имело шесть решений, квадратное уравнение $(∗ )$ должно иметь два различных решения, а каждое полученное кубическое уравнение (из совокупности) должно иметь три различных решения (причем ни одно решение одного уравнения не должно совпадать с каким-либо решением второго!)
Очевидно, что если квадратное уравнение $(∗)$ будет иметь одно решение, то мы никак не получим шесть решений у исходного уравнения.

Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.

1) Чтобы уравнение $(∗)$ имело два различных решения, его дискриминант должен быть положительным:

√ -- √ -- D = a2 − 16a + 52 > 0 ⇔ a ∈ (− ∞; 8 − 2 3) ∪ (8 + 2 3;+ ∞ ) » class=»math-display» width=»auto»></center> </p> <p class=

Таким образом, мы уже обеспечили себе два различных положительных корня $t1$ и $t2$ .

3) Давайте посмотрим на такое уравнение

3 2 √ - x − 3x + 4 = log 2t

При каких $t$ оно будет иметь три различных решения?
Рассмотрим функцию $f(x) = x3 − 3x2 + 4$ .
Можно разложить на множители:

3 2 3 2 2 2 2 x − 3x + 4 = x + x − 4x + 4 = x (x + 1 ) − 4(x + 1)(x − 1) = (x + 1)(x − 2)

Следовательно, ее нули: $x = − 1;2$ .
Если найти производную $′ 2 f (x) = 3x − 6x$ , то мы получим две точки экстремума $xmax = 0,xmin = 2$ .
Следовательно, график выглядит так:
$PIC$
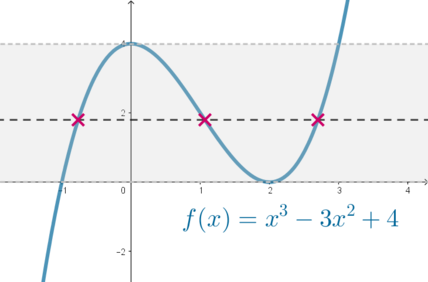
Мы видим, что любая горизонтальная прямая $y = k$ , где $0 < k < 4$ , пересекает график в трех точках. При всех остальных значениях $k$ будет меньше трех точек пересечения. Следовательно, для того, чтобы уравнение $3 2 √ - x − 3x + 4 = log 2t$ имело три различных решения, нужно, чтобы $√ - 0 < log 2t < 4$ .
Таким образом, нужно:

{ 0 < log √2t1 < 4 0 < log √-t < 4 (∗∗) 2 2

Давайте также сразу заметим, что если числа $t1$ и $t2$ различны, то и числа $log√2-t1$ и $log√2 t2$ будут различны, значит, и уравнения $x3 − 3x2 + 4 = log√ -t 2 1$ и $x3 − 3x2 + 4 = log√-t 2 2$ будут иметь несовпадающие между собой корни.
Систему $(∗∗)$ можно переписать так:

{ 1 < t1 < 4 1 < t2 < 4

Таким образом, мы определили, что оба корня уравнения $(∗)$ должны лежать в интервале $(1;4)$ . Как записать это условие?
В явном виде выписывать корни мы не будем.
Рассмотрим функцию $g(t) = t2 + (a − 10)t + 12 − a$ . Ее график – парабола с ветвями вверх, которая имеет две точки пересечения с осью абсцисс (это условие мы записали в пункте 1)). Как должен выглядеть ее график, чтобы точки пересечения с осью абсцисс были в интервале $(1; 4)$ ? Так:
$PIC$
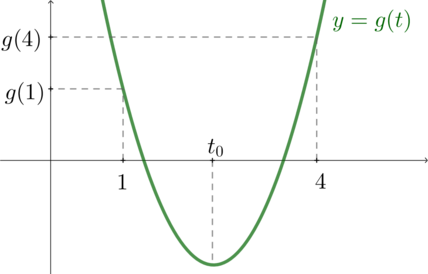
Во-первых, значения $g(1)$ и $g(4)$ функции в точках $1$ и $4$ должны быть положительными, во-вторых, вершина параболы $t0$ должна также находиться в интервале $(1; 4)$ . Следовательно, можно записать систему: