Задача к ЕГЭ на тему «Графика. Нахождение касательной к графику» №9

Автор admin На чтение 2 мин Просмотров 86

При каких значениях параметра $a$ уравнение

2 x = |x|+ a

имеет ровно два решения?

В левой части имеем параболу $2 y = x .$ Правой части соответствует семейство уголков модуля с вершинами на оси ординат, так как координаты вершины $(0;a).$

$PIC$

Рассмотрим случаи расположения уголка относительно параболы.

В положении $II$ вершина уголка совпадает с началом координат, то есть $a= 0,$ и уголок имеет три точки пересечения с параболой. Этот случай нам не подходит.
Если вершина уголка находится выше положения $II,$ уголок имеет ровно две точки пересечения с параболой: левая ветвь уголка с левой ветвью параболы и правая ветвь уголка с правой ветвью параболы. Этот случай нам подходит.
Между положениями $I$ и $II$ каждая из ветвей уголка имеет ровно две точки пересечения с соответствующей ветвью параболы, суммарно четыре точки пересечения. Этот случай нам не подходит.
Если вершина уголка находится в положении $I,$ ветви уголка касаются параболы. Этот случай нам подходит, так как уголок имеет ровно две точки пересечения с параболой.

$PIC$

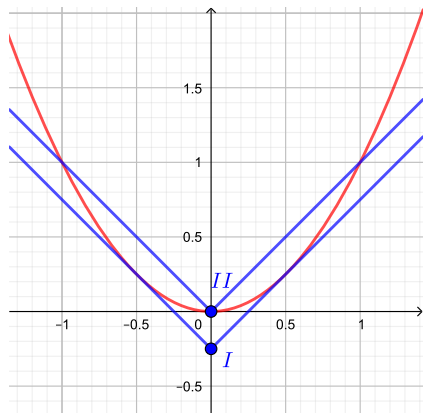
Найдем координаты вершины уголка в положении $I.$ В этом положении правая ветвь уголка, которая описывается уравнением $y = x+ a,$ касается параболы, тогда из симметрии картинки и левая ветвь тоже касается. Запишем критерий касания функций $f(x)= x2$ и $g(x)= x+ a,$ чтобы найти $a:$
$({ ({ 2 f(x)= g(x) ⇔ x =x + a ⇔ (f′(x)= g′(x) (2x =1$ $(( 1)2 1 |{ 2 = 2 + a 1 1 ⇔ |( 1 ⇔ x = 2, a =− 4 x = 2$
Если вершина уголка находится ниже положения $I,$ то уголок не имеет точек пересечения с параболой. Этот случай нам не подходит.

Объединяя все подходящие $a,$ получаем

{ } a ∈ − 1 ∪ (0;+∞ ) 4