Высоты 



а) Докажите, что 
б) Найдите 


а) Из прямоугольного 

Из прямоугольного 

Так как 

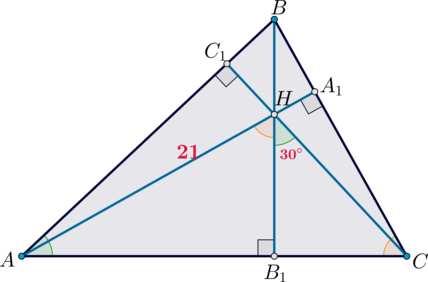
б) Аналогично пункту а) можно доказать, что 
Тогда из прямоугольного 

Заметим, что 

Высоты 



а) Докажите, что 
б) Найдите 


а) Из прямоугольного 

Из прямоугольного 

Так как 


б) Аналогично пункту а) можно доказать, что 
Тогда из прямоугольного 

Заметим, что 
