Задача к ЕГЭ на тему «из прошлых лет» №126

Автор admin На чтение 1 мин Просмотров 29

Решите неравенство

x x 9-⋅ 4x-−-288 8 − 3 ⋅ 4 + 2x − 9 ≤ 32

Сделаем замену $2x = t > 0 » class=»math» width=»auto»><span class=$ :

3 2 9t2 −-288 t − 3t + t − 9 ≤ 32

ОДЗ:

t ⁄= 9

Перенесём всё влево и приведём к общему знаменателю

t4 − 12t3 + 36t2 − 32t t3 − 12t2 + 36t − 32 --------t −-9---------≤ 0 ⇔ t ⋅-------t −-9--------≤ 0

Разложим многочлен третьей степени в числителе левой части последнего неравенства на множители. Можно угадать его корень $t = 2$ . Знание корня многочлена позволяет поделить его столбиком на $t − t0$ , где $t0$ – корень, тогда

| t3 − 12t2 + 36t − 32 |----t-−-2----- t3-−--2t2- | t2 − 10t + 16 − 10t2 + 36t | − 10t2 + 20t | --------16t − 32 | | 16t −-320- | |

тогда последнее неравенство равносильно

t(t-−-2)2(t −-8) t − 9 ≤ 0

По методу интервалов

$PIC$

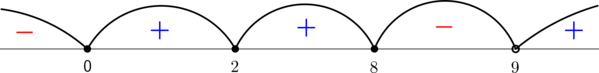
откуда $t ∈ (− ∞; 0] ∪ {2} ∪ [8; 9)$
с учётом ОДЗ и условия $t > 0 » class=»math» width=»auto»>: <img decoding=$
в исходных переменных:

x ∈ {1} ∪ [3;log29 )