Задача к ЕГЭ на тему «из прошлых лет» №162

Автор admin На чтение 1 мин Просмотров 42

а) Решите уравнение $-cosx--= 1− sin x. 1+ sin x$

б) Найдите все корни данного уравнения, принадлежащие отрезку $[ ] 2π; 7π . 2$

а) Перепишем уравнение в следующем виде:

cosx-− (1−-sinx)(1+-sinx) = 0 ⇔ 1+ sinx {cosx− cos2x = 0 ⇔ sinx ⁄= −1 ([ { ccoossxx== 01 (sin x⁄= −1

Пересечем решения данной системы по окружности:

$PIC$

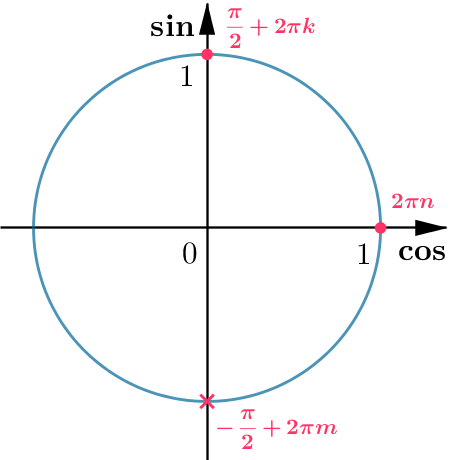
Таким образом, мы видим, что нам подходят только точки $x= 2πn,$ $π x = 2-+2πk$ , $n,k ∈ ℤ.$

б) Отберем корни с помощью неравенств.

7π- 7 2π ≤ 2πn≤ 2 ⇔ 1≤ n ≤ 4 ⇒ n = 1 ⇒ x= 2π π- 7π 3 3 5π 2π ≤ 2 + 2πk ≤ 2 ⇔ 4 ≤ k ≤ 2 ⇒ k = 1 ⇒ x = 2