Страховой фонд владеет акциями, стоимость которых равна 
тыс. рублей в конце каждого года с номером 
где 
Фонд может продать все акции в конце некоторого года и положить все вырученные с продажи средства на счет в банке. Известно, что тогда в конце каждого следующего года банк будет увеличивать сумму, находящую на счете, в 
раз, где 
— некоторое положительное большее единицы число. Оказалось, что если фонд продаст все акции и вложит деньги в банк именно в конце 21-ого года, то в конце 25-ого года он получит наибольшую из возможных прибыль. Определите, какие при этом значения может принимать число 
Если фонд продаст акции в конце 
-ого года, то на конец 25-ого года они пролежат в банке 
лет. Так как каждый год банк увеличивает сумму в 
раз, то за 
лет он увеличит ее в 
раз. Следовательно, на конец 25-ого года фонд будет иметь сумму в тыс. рублей, равную
Рассмотрим эту функцию. В ней 
— некоторое конкретное, но неизвестное число, а 
— переменная. Найдем ее производную:
Таким образом, нулем производной, учитывая, что 
является 
Причем заметим, что эта точка является точкой максимума. Следовательно, до 
функция возрастает, а после — убывает.
Таким образом, если, продав акции в 21-ый год, фонд получит наибольшую из возможных прибыль, то это значит, что мы имеем такой график:
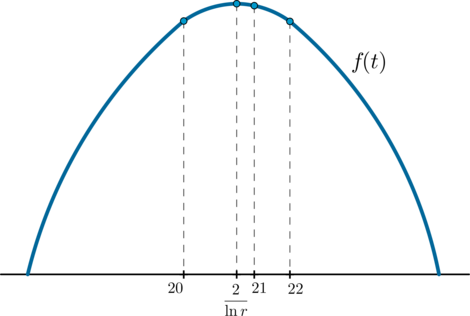
Для примера на картинке точка 
находится правее точки максимума. Может быть наоборот: 21 будет находиться левее точки максимума. Главное, что точка графика с абсциссой 21 выше, чем точки графика с абсциссами 20 или 22!
Тогда f(22). » class=»math» src=»/images/math/answer/answer-930-16.svg» width=»auto»> Из этого условия будет следовать, что
от 1 до 25. Решим полученную систему:
