Задача к ЕГЭ на тему «из прошлых лет» №99
Автор admin На чтение 1 мин Просмотров 31
ОДЗ логарифмов:
![x> 0. » class=»math-display» src=»/images/math/answer/answer-1648-1.svg» width=»auto»></div>
<p class=]() Сделаем замену
Сделаем замену 
, тогда
Решим это неравенство методом интервалов:
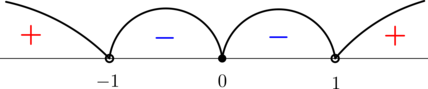
откуда  .
.
 , что можно представить в виде
, что можно представить в виде
![lgx < −1 или lgx =0 или lgx > 1. » class=»math-display» src=»/images/math/answer/answer-1648-7.svg» width=»auto»></div>
<p class=]()
Решим первое неравенство:
Это неравенство на ОДЗ равносильно:
Решим второе уравнение:
Это уравнение на ОДЗ равносильно:
Решим третье неравенство:
![lgx > 1. » class=»math-display» src=»/images/math/answer/answer-1648-12.svg» width=»auto»></div>
<p class=]()
Это неравенство
на ОДЗ равносильно:
![x >10. » class=»math-display» src=»/images/math/answer/answer-1648-13.svg» width=»auto»></div>
<p class=]()
Объединенное решение двух неравенств и уравнения:

.
Пересечем ответ с ОДЗ:
Точки и — середины ребер соответственно и треугольной
87
При каких значениях параметра уравнение имеет ровно
86
При каких значениях параметра уравнение имеет бесконечно
102
При каких значениях параметра касаются графики, задаваемые
84
Решите уравнение Показать ответ
65
На доску слева направо в ряд выписали пять натуральных чисел.
65
Найдите все значения при каждом из которых система
78
Решите неравенство Показать ответ По определению и
71

 , тогда
, тогда

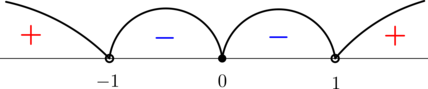






 .
.
