Задача к ЕГЭ на тему «Метод объемов» №1

Найдем расстояние от точки до плоскости через объем пирамиды

Так как призма правильная, то боковые грани — равные прямоугольники. Следовательно, так как то откуда

Следовательно, если — точка пересечения диагоналей и то как медиана и высота в равнобедренном треугольнике.

Пусть — середина Тогда Значит, так как то Отсюда прямая перпендикулярна двум пересекающимся прямым и плоскости Следовательно, Значит, — высота пирамиды проведенная к основанию

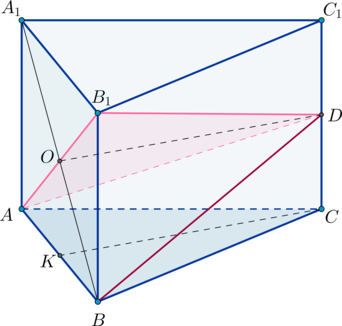
Запишем объем пирамиды двумя способами:

Здесь — расстояние от точки до плоскости

Вычислим длину отрезка и площади треугольников в уравнении выше.

Отрезки как противоположные стороны параллелограмма в котором Тогда имеем:

Тогда искомое расстояние равно