Решите неравенство

ОДЗ:
 Так как
Так как  , то
, то  .
.Обозначим


1)



По методу интервалов:

откуда ![[ √ --- ) ( √---] 14 14 x ∈ − 1 − -----;− 2 ∪ − 2;− 1 + ----- ∪ [1; +∞ ) 2 2](/images/math/answer/answer-1640-10.svg)
Пересечем с условием
2) 


По методу интервалов:
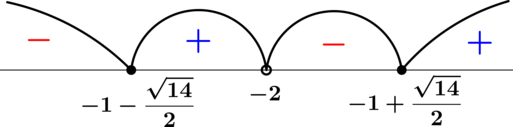
откуда ![( ] ( ] √14-- √14-- x ∈ − ∞; − 1 − ----- ∪ − 2;− 1 + ----- 2 2](/images/math/answer/answer-1640-17.svg)
Пересечем с условием 
![( √---] x ∈ − ∞; − 1 − -14-- 2](/images/math/answer/answer-1640-19.svg)
Объединенное решение двух случаев: ![( √ ---] ( √ ---] x ∈ − ∞; − 1 − --14- ∪ − 2;− 1 + --14- ∪ [1;+ ∞ ) 2 2](/images/math/answer/answer-1640-20.svg)
Пересечем ответ с ОДЗ: ![( √ --] ( √ ---] x ∈ − ∞; − 1 − --14- ∪ − 1 + √3;-− 1 +--14- ∪ [1;+ ∞ ) 2 2](/images/math/answer/answer-1640-21.svg)
Окончательный ответ
![( √ ---] ( √ -- √ --] x ∈ − ∞; − 1 − --14- ∪ − 1 + 3;− 1 + --14- ∪ [1;+ ∞ ). 2 2](/images/math/answer/answer-1640-22.svg)

