Найдите наибольшее значение функции

![[− 3;3]](/images/math/quest/quest-2455-2.svg)
1) 
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна 

 ,
,  . Корни уравнения после замены:
. Корни уравнения после замены:  , откуда находим
, откуда находим  . Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
. Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства 
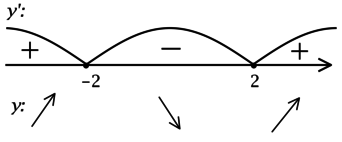
3) Найдём промежутки знакопостоянства 
![[− 3;3]](/images/math/answer/answer-2455-11.svg)
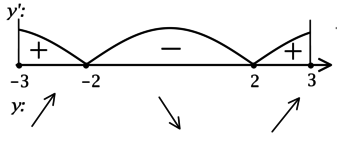
4) Эскиз графика 
![[− 3;3]](/images/math/answer/answer-2455-14.svg)
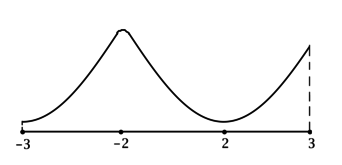
Значит 



Итого: 

![[− 3;3]](/images/math/answer/answer-2455-22.svg)
