Через концы диаметра окружности проведены две пересекающиеся на окружности хорды, сумма длин которых равна 14. Найдите сумму длин расстояний от центра окружности до этих хорд.
Пусть 
— диаметр, 
— центр окружности, 
и 
— хорды, 
Так как 
— вписанный и опирающийся на диаметр, то 
Проведем 
В четырехугольнике 
три угла прямые, следовательно, по признаку он является прямоугольником. Таким образом,
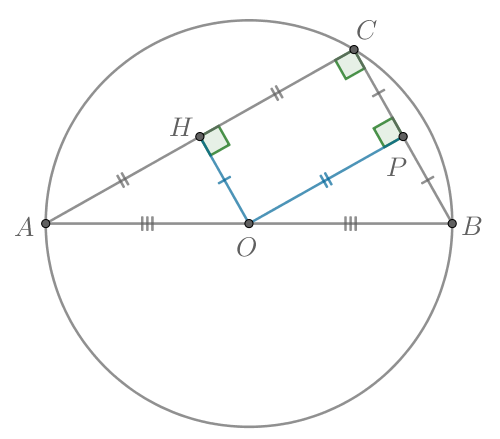
Заметим, что так как перпендикуляр из центра окружности к хорде делит ее пополам, то
Тогда имеем:
