





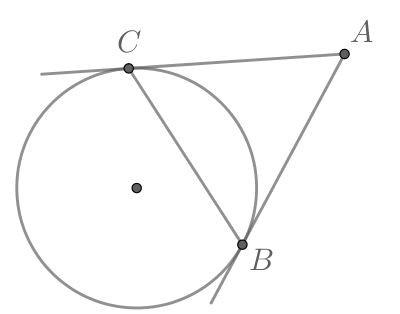
Отрезки касательных, проведённых из одной точки, равны: 



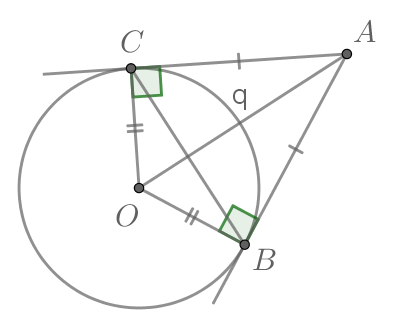
Так как радиус, проведённый в точку касания, перпендикулярен касательной, то 









Таким образом, треугольник 








Отрезки касательных, проведённых из одной точки, равны: 




Так как радиус, проведённый в точку касания, перпендикулярен касательной, то 









Таким образом, треугольник 
