Задача к ЕГЭ на тему «Окружность: углы, образованные хордами, секущими, касательными» №17

Автор admin На чтение 1 мин Просмотров 29

На рисунке диаметр $AB$ пересекает хорду $P T$ и делит ее пополам, а также пересекает хорду $KT.$ Дуга $P B,$ меньшая полуокружности, равна $75∘.$ Дуга $AK,$ меньшая полуокружности, равна $15∘.$

$PIC$

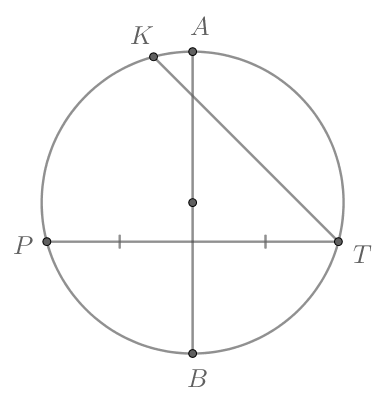
Найдите угол между прямыми $AB$ и $KT.$ Ответ дайте в градусах.

Рассмотрим картинку:

$PIC$

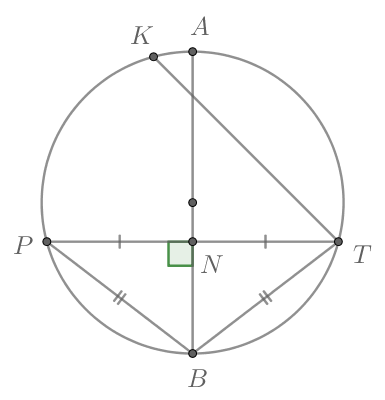
Так как диаметр, делящий хорду пополам, перпендикулярен ей, то $AB ⊥ P T.$ Следовательно, $△P NB = △T NB$ как прямоугольные по двум катетам ( $PN = T N,$ $NB$ — общий). Отсюда получаем $P B = TB.$

Так как равные хорды стягивают равные дуги, то

⌣ ⌣ TB= PB= 75∘

Тогда угол между хордами $AB$ и $KT$ равен полусумме дуг, заключенных между ними, то есть

∘ ∘ ∘ 0,5 (15 + 75 )= 45

Так как нам необходимо найти угол между прямыми (а это обязательно нетупой угол), то в данном случае он равен углу между данными хордами.

Окружность: углы, образованные хордами, секущими, касательными

admin

Оцените автора

Добавить комментарий