Из точки 
вне окружности проведены две касательные 
и 
Через произвольную точку 
на окружности проведена касательная к окружности, пересекающая 
и 
в точках 
и 
соответственно. Найдите угол 
если 
Ответ дайте в градусах.
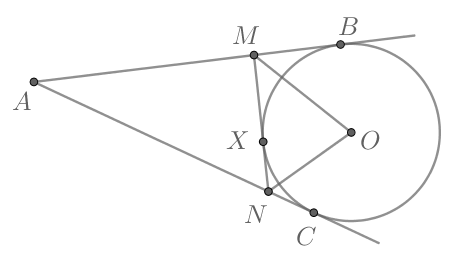
Рассмотрим картинку (пусть 
— точки касания):
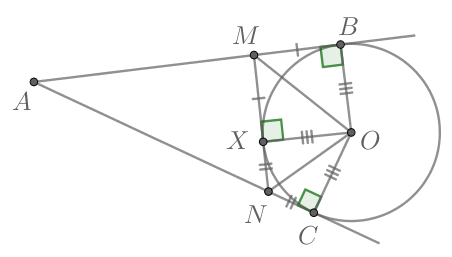
Т.к. отрезки касательных, проведенные из одной точки, равны, то 
и 
Т.к. радиусы, проведенные в точку касания, перпендикулярны касательной, то
Таким образом, по двум катетам равны треугольники: 
и 
Значит, 
и 
Следовательно, 
Т.к. в четырехугольнике сумма углов равна 
то в четырехугольнике 
Следовательно,
