Задача к ЕГЭ на тему «Окружность: углы, образованные хордами, секущими, касательными» №22

Автор На чтение 1 мин Просмотров 29

Угол между хордой AB и касательной BC к окружности равен 32∘. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

PIC

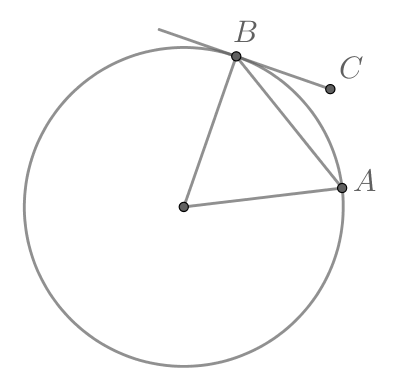
1 способ.

Так как угол между хордой и касательной, проведенными из одной точки окружности, равен половине дуги, заключенной между ними, то меньшая дуга A⌣B равна 2⋅32∘ = 64∘.

2 способ.

PIC

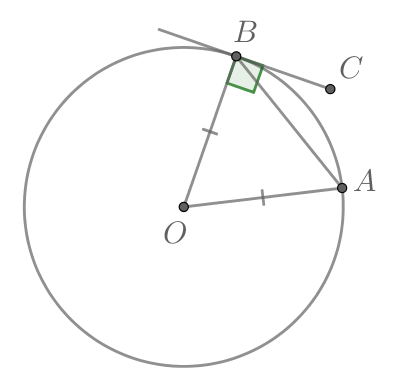
Так как радиус, проведенный в точку касания, перпендикулярен касательной, то ∠OBC = 90∘. Следовательно,

∠OBA = 90∘ − 32∘ = 58∘

Так как OB = OA — радиусы, то треугольник OBA равнобедренный, следовательно,

∠AOB = 180∘− 2⋅58∘ = 64∘

Так как дуга равна центральному углу, опирающемуся на нее, то меньшая дуга ⌣ AB равна ∠AOB и равна 64∘.

Окружность: углы, образованные хордами, секущими, касательными
admin
Оцените автора
Я решу все!
Добавить комментарий

© 2025 Я решу все!