Угол 







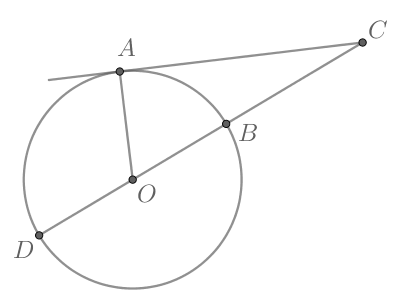
Найдем градусную меру меньшей дуги, стягиваемой хордой 

Так как радиус, проведенный в точку касания, перпендикулярен касательной, то 


Тогда имеем:

Дуга 



Угол 








Найдем градусную меру меньшей дуги, стягиваемой хордой 

Так как радиус, проведенный в точку касания, перпендикулярен касательной, то 


Тогда имеем:

Дуга 


