К окружности, вписанной в треугольник 



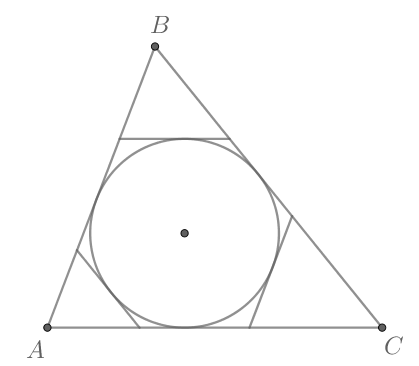
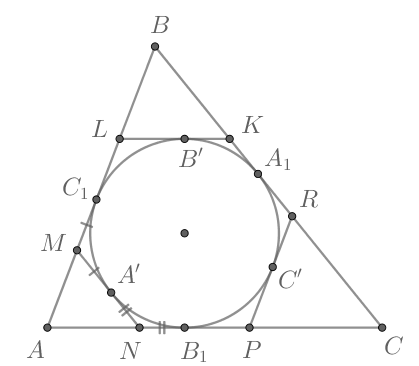
Рассмотрим рисунок. Пусть 




Так как отрезки касательных, проведенных из одной точки к окружности, равны, то 

Аналогично для других треугольников:

Следовательно,

К окружности, вписанной в треугольник 





Рассмотрим рисунок. Пусть 




Так как отрезки касательных, проведенных из одной точки к окружности, равны, то 

Аналогично для других треугольников:

Следовательно,
