В основании пирамиды 







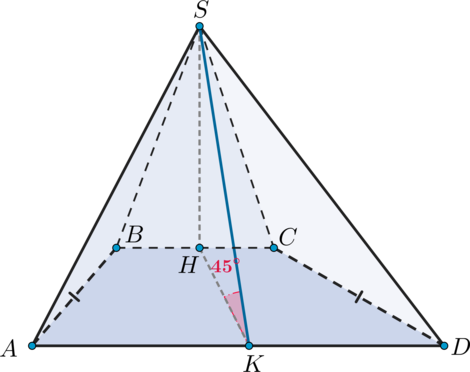
Пусть 










 также высота трапеции. Так как площадь трапеции равна полусумме оснований, умноженной на высоту, а полусумма оснований в свою очередь равна средней линии, то
также высота трапеции. Так как площадь трапеции равна полусумме оснований, умноженной на высоту, а полусумма оснований в свою очередь равна средней линии, то 

В основании пирамиды 








Пусть 










 также высота трапеции. Так как площадь трапеции равна полусумме оснований, умноженной на высоту, а полусумма оснований в свою очередь равна средней линии, то
также высота трапеции. Так как площадь трапеции равна полусумме оснований, умноженной на высоту, а полусумма оснований в свою очередь равна средней линии, то 
