Задача к ЕГЭ на тему «Поиск точек экстремума у элементарных функций» №5

Автор admin На чтение 1 мин Просмотров 30

Найдите точку локального минимума функции $y = x1,25 − 5x + 12$ .

ОДЗ: $x ≥ 0$ . Решим на ОДЗ:

1) $y ′ = 1,25x0,25 − 5$ .

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна $0$ или не существует):

1,25x0,25 − 5 = 0 ⇔ 1,25x0,25 = 5.

Возводя последнее уравнение в 4 степень, находим $x = 256$ . Проверкой убеждаемся, что $x = 256$ – корень уравнения $0,25 1,25x − 5 = 0$ .

Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства $y′$ :

$PIC$

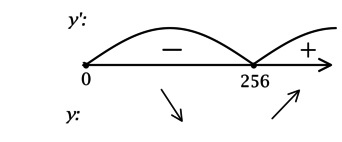
3) Эскиз графика $y$ :

$PIC$

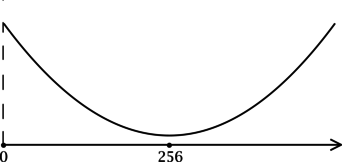
Таким образом, $x = 256$ – точка локального минимума функции $y$ .