Задача к ЕГЭ на тему «Поиск точек экстремума у сложных функций» №11

Автор admin На чтение 1 мин Просмотров 36

Найдите точку минимума функции $y = log (x2− 10x +201). 2016$

Выпишем ОДЗ: x2− 10x +201 >0. » class=»math» src=»/images/math/answer/answer-2420-1.svg» width=»auto»> </p>
<p class= 1) Найдем производную:

1 2x − 10 y′ = ln2016 ⋅ x2− 10x-+201

Найдём критические точки, то есть внутренние точки области определения функции, в которых её производная равна 0 или не существует:

--1---⋅---2x−-10---= 0 ln 2016 x2− 10x+ 201

Отсюда получаем $2x− 10= 0,$ то есть $x = 5.$

Далее имеем:

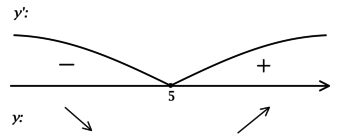
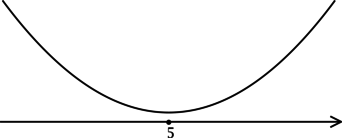
Тогда производная определена для любого Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график. 2) Найдём промежутки знакопостоянства 3) Изобразим эскиз графика Таким образом, — точка минимума функции