Задача к ЕГЭ на тему «Поиск точек экстремума у смешанных функций» №2

Автор admin На чтение 1 мин Просмотров 26

Найдите точку максимума функции

y = x⋅ x-+x-2+-1x e e

на промежутке $[0;2].$

Найдем ОДЗ: $x$ — любое число.

1) Найдем производную функции:

x x y′ = x+ex2+ x ⋅ e-−-ee(2xx+-2)− e1x = x + 2 1 − (x+ 2) 1 1− x2 = --ex--+ x⋅----ex----− ex = -ex--

Найдём критические точки, то есть внутренние точки области определения функции, в которых её производная равна нулю или не существует:

[ 1 − x2 x= − 1 --ex- = 0 ⇔ x= 1

Производная существует при любом $x.$

2) Найдём промежутки знакопостоянства $y′ :$

$PIC$

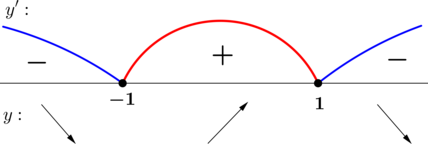
3) Найдём промежутки знакопостоянства $y′$ на рассматриваемом промежутке $[0;2]:$

$PIC$

4) Эскиз графика $y$ на промежутке $[0;2]:$

$PIC$

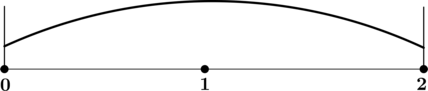
Таким образом, $x = 1$ — точка максимума функции $y$ на промежутке $[0;2].$