Дана прямая призма 







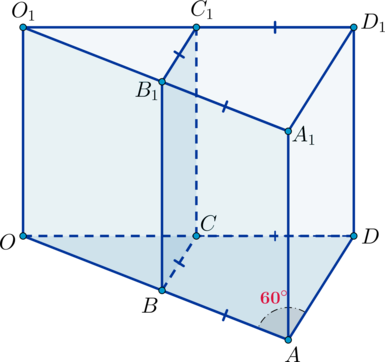
Из условия следует, что нужно найти

 и трапеция равнобедренная, то
и трапеция равнобедренная, то  . Следовательно,
. Следовательно,  равнобедренный с углом при основании
равнобедренный с углом при основании  , значит, равносторонний. Значит,
, значит, равносторонний. Значит,  . Также
. Также  , причем коэффициент подобия равен
, причем коэффициент подобия равен  . Следовательно,
. Следовательно,  . Тогда
. Тогда  . Значит
. Значит 
