Задача к ЕГЭ на тему «Производная в точке касания как тангенс угла наклона касательной» №13

Автор admin На чтение 1 мин Просмотров 37

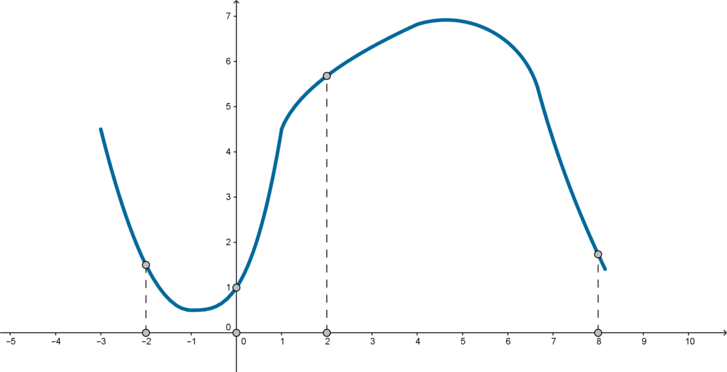
На рисунке изображен график функции $y = f(x)$ и отмечены точки $− 2; 0; 2; 8.$ В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

$PIC$

Проведем касательные к графику функции в этих точках. Так как тангенс угла $α$ наклона касательной равен значению производной $f′(x)$ в точке касания $x0,$ то есть $f′(x0)= tgα,$ то нужно сравнить тангенсы углов, отмеченных на рисунке.

$PIC$

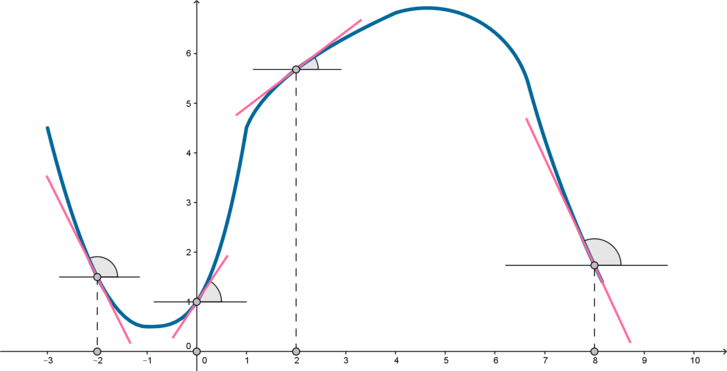
Вспомним, что если угол тупой, то его тангенс отрицательный, если острый — положительный. Следовательно, так как мы ищем наибольший тангенс, то имеет смысл рассматривать только острые углы. Это углы, образованные касательными в точках 0 и 2.

Заметим, что угол в точке 0 больше, следовательно, его тангенс также больше, чем тангенс угла в точке 2. Таким образом, ответ: 0.