В треугольнике 




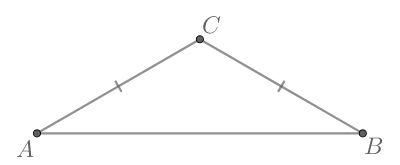
Рассмотрим прямоугольный треугольник 
Так как 


Катет, лежащий напротив угла 


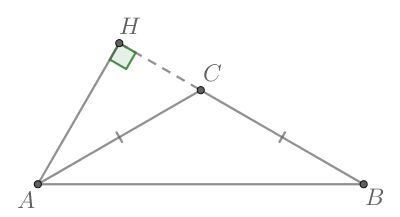
Рассмотрим прямоугольный треугольник 


Так как в прямоугольном треугольнике сумма острых углов равна 

Следовательно, 


В треугольнике 





Рассмотрим прямоугольный треугольник 
Так как 


Катет, лежащий напротив угла 



Рассмотрим прямоугольный треугольник 


Так как в прямоугольном треугольнике сумма острых углов равна 

Следовательно, 

