Дана треугольная пирамида 







Из условия задачи следует, что:



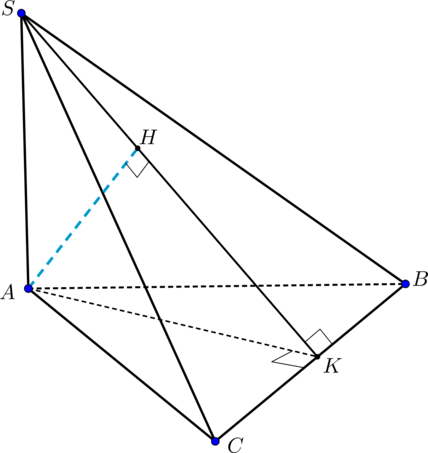
Так как 



Таким образом, перпендикуляр 






По теореме Пифагора в 

Тогда

По теореме Пифагора в 

Дана треугольная пирамида 







Из условия задачи следует, что:




Так как 



Таким образом, перпендикуляр 






По теореме Пифагора в 

Тогда

По теореме Пифагора в 
