Задача к ЕГЭ на тему «Рациональные неравенства и метод интервалов» №21
Автор admin На чтение 1 мин Просмотров 31
Решите неравенство

ОДЗ:

Решим полученное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.
1) Нули числителя находятся из уравнения
 Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл,
Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя:

2) Найдём нули знаменателя:

так как

, то

только при

.
Сравним  и
и  . Так как
. Так как 
 таким образом,
таким образом,  – это знак
– это знак  .
.
По методу интервалов:
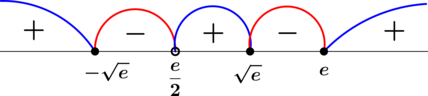
откуда
![[ √ -- e) √ -- x ∈ − e; -- ∪ [ e;e]. 2](/images/math/answer/answer-1199-17.svg)
В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).





 , то
, то  только при
только при  .
.







![[ √ -- e) √ -- x ∈ − e; -- ∪ [ e;e]. 2](/images/math/answer/answer-1199-17.svg)
