Задача к ЕГЭ на тему «Стереометрия» №1

Автор admin На чтение 1 мин Просмотров 27

Дан прямоугольный параллелепипед $ABCDA1B1C1D1$ , в основании которого лежит квадрат $ABCD$ . На ребрах $BB1$ , $CC1$ , $DD1$ отмечены точки $M, N, K$ соответственно так, что $BM : M B1 = 1 : 5$ , $CN : N C1 = 3 : 1$ , $DK : KD1 = 1 : 2$ .
Найдите отношение отрезков, на которые делит плоскость $M N K$ диагональ $AC$ .

Обозначим ребро основания за $a$ , а боковое ребро за $b$ . Тогда из условия задачи следует, что $BM = 16b$ , $CN = 34b$ , $DK = 13b$ .

$PIC$

Найдем положение точек $R$ и $T$ , в которых плоскость пересекает ребра $AB$ и $AD$ соответственно.

1) Продлим отрезки $N K$ и $CD$ до пересечения в точке $Q$ . Тогда $△QDK ∼ △QN C$ . Следовательно,

QD KD QD 1b 4 4 ---- = ---- ⇒ --------= 33--= -- ⇒ QD = -a. QC N C QD + a 4b 9 5

Аналогично из $△OM B ∼ △ON C$ получаем, что

OB = 2a. 7

Соединив точки $Q$ и $O$ , получим точки пересечения плоскости с ребрами $AB$ и $AD$ .

2) Рассмотрим основание.

$PIC$

$△OBR ∼ △OCQ$ , следовательно,

OB-- BR-- 27a- BR-- 2- OC = CQ ⇒ 9a = 9a ⇒ BR = 5 a. 7 5

$△OBR ∼ △T AR$ , следовательно,

2 2 OB--= BR-- ⇒ -7a-= 5a- ⇒ AT = 3a. AT AR AT 3a 7 5

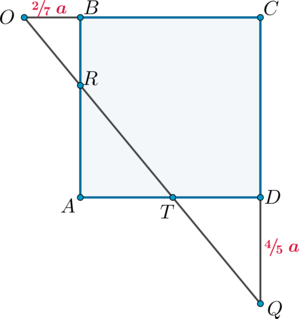
3) Для того, чтобы найти, в каком отношении $RT$ поделит $AC$ , проведем прямую $RG ∥ AD$ , $G ∈ AC$ .

$PIC$

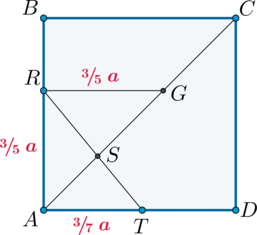
Тогда $△ARG$ – прямоугольный и $∘ ∠RAG = 45$ , то есть он равнобедренный и $3 RG = 5a$ . Тогда по теореме Фалеса $AG : AC = AR : AB = 3 : 5$ , следовательно, т.к. $√ -- AC = a 2$ , то $√- AG = 3-2a 5$ .