В треугольнике 



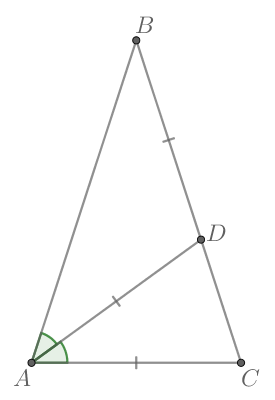
У равнобедренного треугольника углы при основании равны. Так как 

Согласно теореме о внешнем угле треугольника,

Тогда
 — наименьший.
— наименьший.
Так как 

По теореме о сумме углов треугольника

Найдем угол 

В треугольнике 




У равнобедренного треугольника углы при основании равны. Так как 

Согласно теореме о внешнем угле треугольника,

Тогда
 — наименьший.
— наименьший.
Так как 

По теореме о сумме углов треугольника

Найдем угол 
