Дана четырехугольная пирамида, все ребра которой равны, причем основание является квадратом. Найдите 

Пусть 




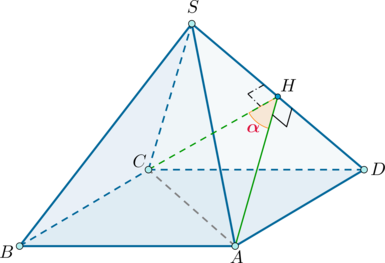
Проведем 






Так как в основании лежит квадрат, то 



Тогда по теореме косинусов из 

Дана четырехугольная пирамида, все ребра которой равны, причем основание является квадратом. Найдите 

Пусть 





Проведем 






Так как в основании лежит квадрат, то 



Тогда по теореме косинусов из 
