В невыпуклом четырёхугольнике 









Косинусы смежных углов противоположны: 
Косинус внешнего угла при вершине 



Так как косинус внешнего угла равен минус косинусу угла, смежного с ним, то косинус внешнего угла при вершине 

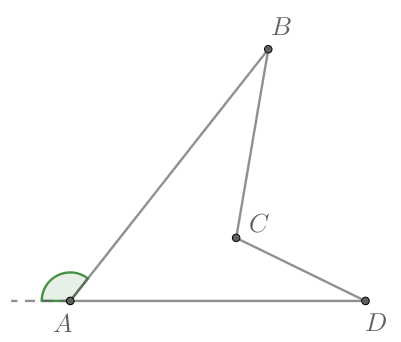
В невыпуклом четырёхугольнике 










Косинусы смежных углов противоположны: 
Косинус внешнего угла при вершине 



Так как косинус внешнего угла равен минус косинусу угла, смежного с ним, то косинус внешнего угла при вершине 
