Угол между двумя высотами остроугольного треугольника 
равен 
, а точка пересечения высот делит одну из них в отношении 
, считая от вершины треугольника.
а) Докажите, что этот треугольник равнобедренный.
б) Пусть 
– радиус описанной около 
окружности, 
– радиус вписанной в 
окружности. Найдите 
, если 
.
а) Пусть 
и 
– высоты треугольника 
, пересекающиеся в точке 
, 
. Построим третью высоту 
(она также пройдёт через точку 
).
, тогда в треугольнике 
катет, лежащий против 
равен половине гипотенузы. Обозначим 
, тогда 
, значит, 
.
Треугольники 
и 
равны по катету и гипотенузе (
– общая), откуда следует, что
и 
равны по катету и острому углу (
– общий), тогда 
.
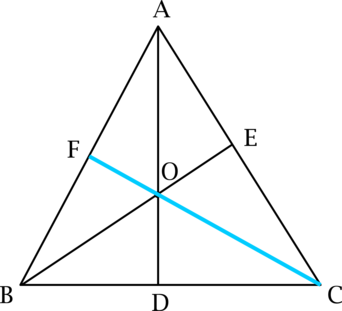
б) Покажем, что 
.
.
Треугольники 
и 
равны по катету и острому углу, откуда 
, тогда, 
, но 
, следовательно,
– равнобедренный треугольник в котором один из углов равен 
, тогда 
– равносторонний треугольник.
Так как 
– равносторонний, то 
– центр вписанной и описанной окружностей, тогда
. Так как 
, то 
, 
, тогда 
, то есть 
