Задача к ЕГЭ на тему «Задачи формата ЕГЭ» №23

Точка $O$ – центр вписанной в трапецию $ABCD$ окружности, которая касается стороны $AB$ в точке $R$ , а стороны $AD$ в точке $T$ . Прямая, содержащая отрезок $BO$ , пересекает сторону $AD$ в точке $S$ .

а) Докажите, что $RT ∥ BS$ .

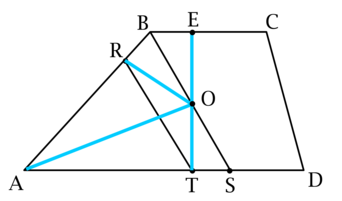
б) Средняя линия трапеции $BCDS$ равна $4$ , а площадь треугольника $COD$ равна 16. Найдите $CO$ .

а) Проведем радиусы $OR$ , $OT$ и радиус $OE$ в точку $E$ касания окружности со стороной $BC$ , а также соединим $A$ и $O$ . $PIC$

Тогда $OE$ перпендикулярно $BC$ и значит точки $B$ , $O$ и $T$ лежат на одной прямой, откуда $∠BOE = ∠T OS$ как вертикальные, следовательно треугольники $BOE$ и $TOS$ равны по катету и острому углу ( $T O = OE$ как радиусы).

Тогда $BO = OS$ . $AO$ – биссектриса в треугольнике $ABS$ (она проходит через точку, равноудаленную от сторон угла $∠BAS$ ), но из равенства $BO = OS$ следует, что $AO$ – медиана.

Треугольник, в котором биссектриса является медианой – равнобедренный и $AO$ перпендикулярна $BS$ .

$AR = AT$ как отрезки касательной, проведенной из одной точки, тогда треугольники $ARO$ и $AOT$ – равны (по трем сторонам), тогда $∠AOR = ∠AOT$ и $AO$ – биссектриса угла $∠ROT$ .

Треугольник $ROT$ равнобедренный, тогда $AO$ перпендикулярна $RT$ . В итоге, $AO$ перпендикулярна $RT$ и $BS$ , тогда $RT ∥ BS$ .

б) Пусть $OK$ – перпендикуляр из точки $O$ на $CD$ . Средняя линия трапеции $BCDS$ является средней линией трапеции $ECT D$ .

Так как средняя линия трапеции равна полусумме оснований, то

EC + TD = 2 ⋅ 4 = 8.

$CD = EC + T D = 8$ (так как отрезки касательных, проведенных из одной точки равны, то $EC = CK$ , а $T D = DK$ ).

S = 1CD ⋅ OK = 16, COD 2

откуда $OK = 4$ , следовательно $OK$ и есть средняя линия трапеции $BCDS$ (перпендикуляр из точки на прямую имеет наименьшую длину, другой отрезок, соединяющий $O$ и точку на $CD$ был бы длиннее).

$OK$ перпендикулярен $CD$ , но $OK ∥ AD$ , тогда $ABCD$ – прямоугольная трапеция, $∠ADC = 90 ∘$ . В итоге $OECK$ – прямоугольник, у которого $OE = OK = 4$ , тогда он квадрат и $OK = CK = 4$ .

Треугольник $COK$ – прямоугольный, тогда $-- CO = 4√ 2$ .