Прямая, проходящая через вершину 






a) Докажите, что 
б) Найдите расстояние от центра прямоугольника до прямой 

(МИОО 2017)
а) Обозначим 









Тогда четырехугольник 


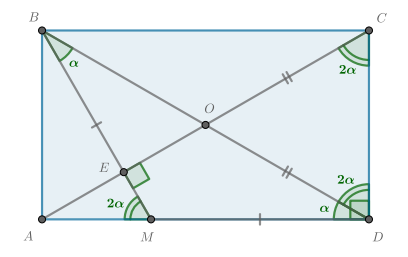
В прямоугольнике диагонали равны, значит

Найдем угол 

Тогда

б) Пусть точка 









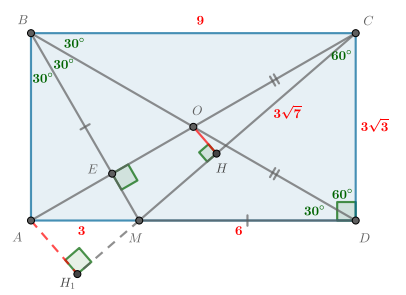
Найдем длины некоторых отрезков, воспользовавшись условием, что 

Запишем площадь треугольника 

Отсюда найдем искомое расстоние 

