Задача по механике №127

Два корабля двигаются в море со скоростями $v1 = 15 м/с$ и $v2 = 30 м/ с,$ при этом скорости направлены таким образом, что траектории кораблей пересекаются под углом $α = 60∘ :$

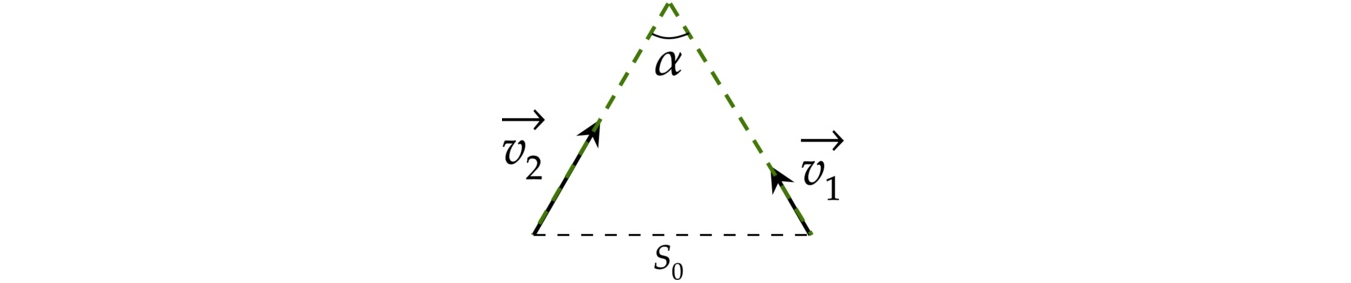
Корабли расположены таким образом, что расстояние между кораблями равно $S0 = 20 км,$ расстояния между кораблями и точкой пересечения траекторий равны. Через некоторое время расстояние между кораблями становится минимальным. Найдите это расстояние.

I способ

Перейдем в систему отсчета, связанную с первым кораблем.
Тогда относительная скорость равна

v⃗отн = ⃗v2 − ⃗v1

Чтобы найти угол $β$ рассмотрим треугольник со сторонами $v1,v2,v отн$

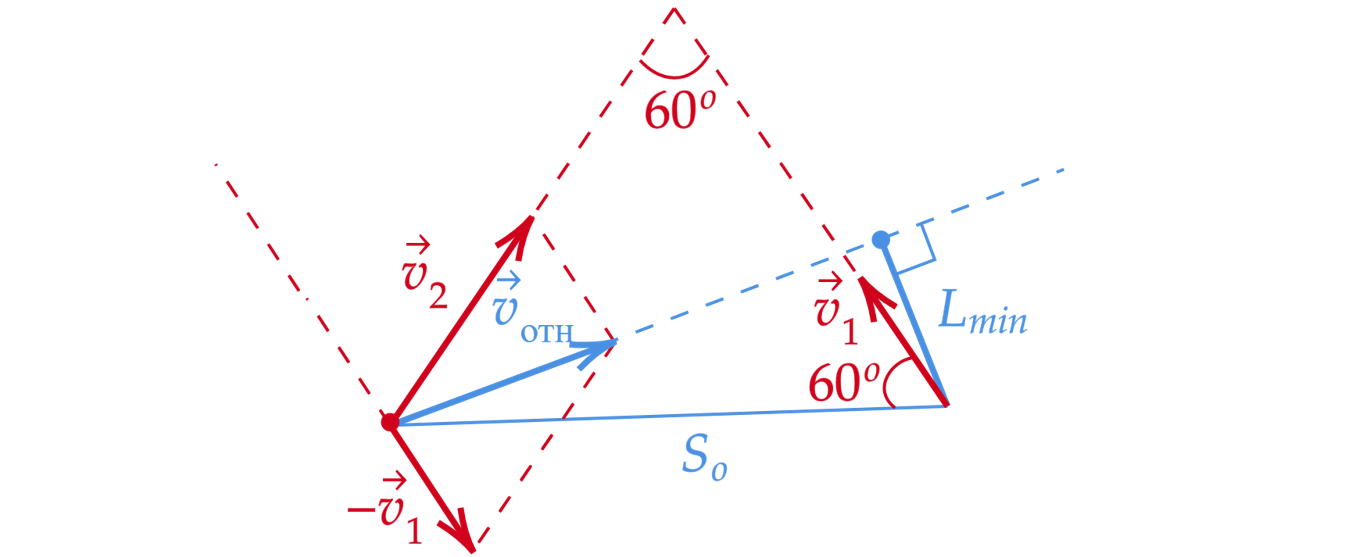
Угол между сторонами $v1$ и $v2$ равен $60∘.$

По теореме косинусов

∘ ------------------- v = v2 +v2 − 2vv cos60∘ = 26 м/с отн 1 2 12

По теореме синусов найдем $γ$

v1 v отн v1sin 60∘ 1 sin-γ = sin60∘-⇒ sinγ = --v отн-= 2

А угол $β$ равен $60∘ − 30∘ = 30∘$ , значит, траектория относительного движения является биссектрисой, а в равностороннем треугольнике она является еще и медианой, следовательно, $L = S0-= 10 км min 2$

___________________________________________________________________________________________________

II способ
До момента пересечения траекторий корабли будут сближаться, после пересечения траекторий корабли будут удаляться. Значит, минимальное расстояние в точке пересечения траекторий. Так как скорость второго в 2 раза больше, чем скорость первого, то он придет в точку пересечения в 2 раза быстрее, а расстояние между кораблями будет равно половине траектории. Заметим, что треугольник равносторонний (равнобедренный, с углом при пересечении одинаковых ребер 60 градусов), значит длина траектории равна $S = 20 км. 0$ Так как расстояние между кораблями равно $S0 -2-= 10 км.$