Задача по оптике №25

Автор admin На чтение 1 мин Просмотров 44

При повороте плоского зеркала на некоторый угол вокруг оси, проходящей через точку падения луча перпендикулярно плоскости, в которой лежат падающий и отраженный лучи, угол между падающим и отраженным лучами увеличился на $40∘$ . На какой угол (в градусах) было повернуто зеркало?

При повороте зеркала на угол $α$ , угол между падающим и отраженным лучами увеличивается на $2α$ , следовательно, зеркало было повернуто на $20∘$ . Докажем это:

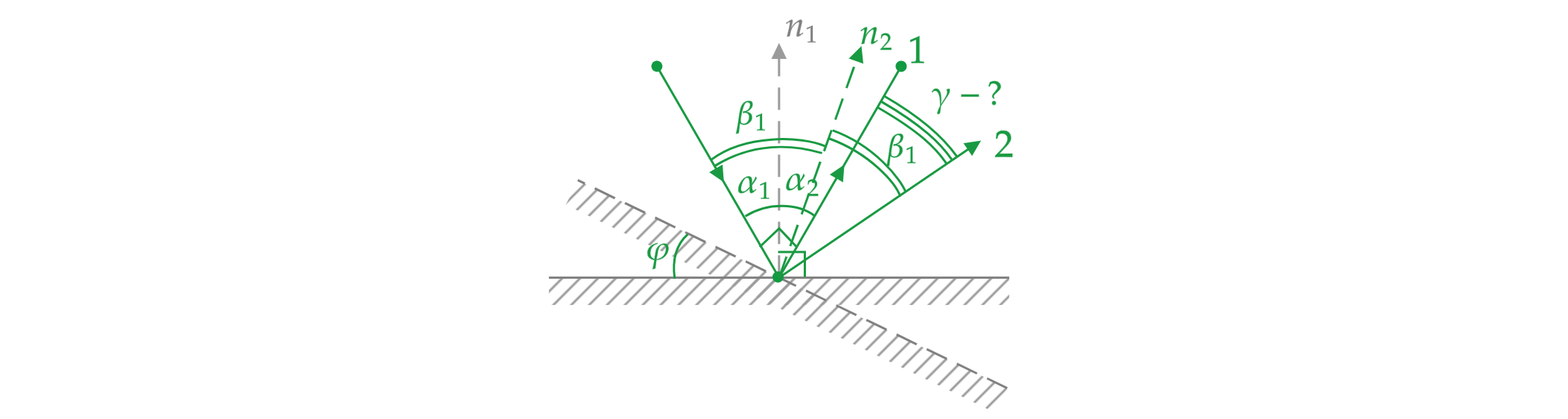
Рассмотрим нашу ситуацию. Пусть $n1$ — перпендикуляр к отражающей поверхности в 1 случае, $n2$ — перпендикуляр к отражающей поверхности после поворота.
Пусть угол падения в 1 случае равен $α1$ . Угол отражения(1) $α2 = α1 = α$ .
Пусть угол падения после поворота: $β1 =α + φ$ . Угол отражения в этом случае (2) $β1$ .
Чтобы доказать, что при повороте на угол $α$ , угол между падающим и отраженным лучами увеличивается на $2α$ , т.к. угол падения не меняет своего расположения требуется доказать, что угол между лучом (1) и лучом (2) равен 2 $α$ .
Обозначим этот угол как $γ$ . Пусть угол между лучом 1 и $n2$ равен $δ$ .

γ = β1− δ =β1 − (α − φ) =α + φ− α +φ = 2φ

ч.т.д.